ML - Week 10 - Theoretical Exercises¶
Graphical Models¶
As explained in the note Coditional probabilites and graphical, a graphical model is a graphical notation to describe the dependency relationships when specifying a joint probility.
From graph to joint probability¶
For the following four graphs, write down the joint probabilty of the random variables.
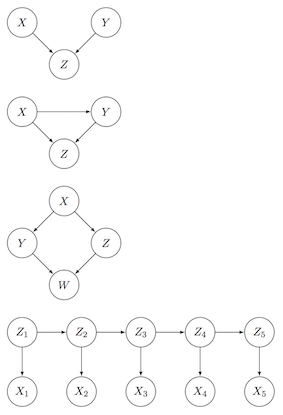
From joint probability to graph¶
Draw the following four joint probabilities as dependency graphs.
$p(X)p(Y)p(Z)$
$p(X)p(Y\,|\,X)p(Z\,|\,X)$
$p(X)p(Y\,|\,X)p(Z\,|\,Y)p(W\,|\,X,Z)$
$p(Z_1)\prod_{i=1}^{5}p(X_i\,|\,Z_i)\prod_{i=2}^{5}p(Z_i\,|\,Z_{i-1})$
Hidden Markov Models¶
Questions to slides Hidden Markov Models - Terminology, Representation and Basic Problems:
How much time does it take to compute the joint probability $P({\bf X}, {\bf Z})$ in terms of $N$ and $K$?
How many terms are there in the sum on slide 31 for computing $P({\bf X}|\Theta)$? Does the sum yield an efficient algorithm?
How many terms are there in the maximization on slide 34 for computing the Viterbi decoding ${\bf Z}^*$?
How many terms are there in the maximixation on slide 34 for computing ${\bf z}^*_n$, i.e. the nth state in a posterior decoding?
Questions to slides Hidden Markov Models - Algorithms for decoding:
Where in the derivation of $\omega({\bf z}_n$) on slide 6 do we use that the fact that we are working with hidden Markov models?
Where in the derivation of $p({\bf z}_n | {\bf x}_1, \ldots, {\bf x}_N)$ on slide 15 do we use the fact that we are working with hidden Markov models?
Where in the derivation of $\alpha({\bf z}_n)$ and $\beta({\bf z}_n)$ on slide 19 and 25 do we use that the fact that we are working with hidden Markov models?
Why is $\sum_{{\bf z}_n} \alpha({\bf z}_n) \beta({\bf z}_n) = \sum_{{\bf z}_N} \alpha({\bf z}_N)$ as stated on slide 30?
Can you find other (small) examples of hidden Markov models and inputs where Viterbi and posterior decoding differs like in the example on slide 33?
Algorithmic question: Slide 34 shows how to compute $P({\bf X})$ from $\alpha({\bf z}_N)$ in time $O(K^2N)$, i.e. the time it takes to compute the last (rightmost) colummn in the $\alpha$-table. How much space do you need to compute this column? Do you need to store the entire $\alpha$-table?